The intrinsic relationship between mathematics and the physical sciences is nowhere more evident than in the field of semiconductor physics, where the mathematical constant π plays a pivotal role in describing and predicting the behaviour of charge carriers within semiconductor materials.
This article delves into the fascinating world of π within semiconductor physics, focusing on its crucial applications in carrier concentration equations and the dynamics of electrons and holes.
Semiconductor fundamentals and the role of π
Semiconductors, materials with electrical conductivity intermediate between conductors and insulators, are the backbone of modern electronics. The electrical properties of semiconductors are primarily governed by the movement and interaction of charge carriers, namely, electrons and holes. The distribution of these carriers across energy bands is a fundamental aspect of semiconductor behaviour, influencing everything from the material’s conductivity to its response to external stimuli.
Carrier concentration in semiconductors, a measure of the number of charge carriers per unit volume, is critical for understanding and designing semiconductor devices. The calculation of carrier concentrations involves statistical mechanics, where π emerges as a fundamental component, particularly in the Fermi-Dirac distribution and the effective density of states in the conduction and valence bands.
Carrier concentration and Fermi-Dirac statistics
The Fermi-Dirac distribution, f(E), describes the probability that an energy state E is occupied by an electron at a given temperature. It is given by:
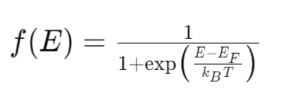
where EF is the Fermi level, kB is the Boltzmann constant, and T is the temperature in Kelvin. The expression for f(E) does not explicitly contain π; however, π is inherently present in the calculation of the Fermi level and the density of states for electrons and holes, influencing the distribution of charge carriers in semiconductors.
Effective density of states
The effective density of states in the conduction (NC) and valence (NV) bands quantifies the number of available states for electrons and holes, respectively. These are given by:
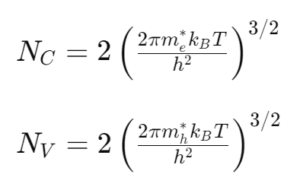
where m*e and m*h are the effective masses of electrons and holes, respectively, and h is Planck’s constant. Here, π is explicitly present, underscoring its significance in determining the density of available states for charge carriers.
Carrier concentration equations
The carrier concentrations, n for electrons and p for holes, can be derived from the effective density of states and the Fermi-Dirac distribution, resulting in:
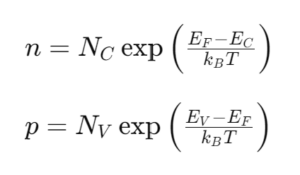
where EC and EV are the conduction band minimum and valence band maximum, respectively. Through the effective density of states expressions, π indirectly influences these carrier concentration equations, affecting the electrical properties of semiconductors.
π in semiconductor equations and device physics
Beyond carrier concentration, π is also found in other semiconductor equations, such as the Schrödinger equation for particle wave functions and the Poisson equation for electrostatics within semiconductor structures. These equations are fundamental for understanding the quantum mechanical and electrostatic behaviour of semiconductors, guiding the design and analysis of semiconductor devices.
In device physics, π’s influence extends to the operation of diodes, transistors, and other semiconductor components. For instance, in the analysis of p-n junctions, π appears in the calculation of depletion regions and the capacitance of junctions, which are crucial for the device’s switching behaviour and response to applied voltages.
Conclusion
The constant π is deeply ingrained in the mathematical framework that describes semiconductor physics. Through its presence in the calculation of effective density of states, carrier concentrations, and beyond, π enables a deeper understanding of the behaviour of electrons and holes in semiconductor materials. This understanding is paramount for the development of electronic devices that underpin modern technology. As we continue to push the boundaries of what is possible in semiconductor technology, the role of mathematical constants like π reminds us of the intrinsic connection between abstract mathematics and tangible technological advancements.




