RLC circuits analysis and quality factor

Let’s consider series and parallel RLC circuits with lumped parameters. They can be used for modelling resonators.

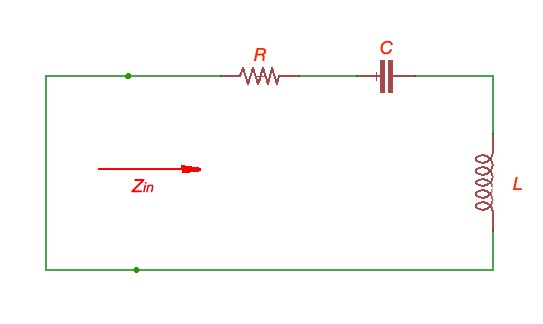
RLC series resonant circuit.

Here $Z_{i n} = R + j w L - \frac{j}{w C}$ . Input resonator power is $P_{i n} = \frac{V I}{2} = \frac{Z_{i n} I^{2}}{2} = \frac{I^{2}}{2} (R + j w L - \frac{j}{w C})$ . Power, loss on the resistor $R$ is $P_{l o s s} = \frac{I^{2} R}{2}$ , power stored at the inductor is $P_{L} = \frac{I^{2} R}{4}$ . Power stored at capacitor is $P_{C} = \frac{I^{2}}{4 w^{2} C}$ . Then $P_{i n} = P_{l o s s} + 2 j w (P_{L} - P_{C})$ and $Z_{i n} = \frac{2 P_{i n}}{I^{2}}$ .

Resonance happens when $P_{L} = P_{C}$ , then $Z_{i n} = R$ when $w_{0} = \frac{1}{\sqrt{L C}}$ .

Resonant circuit can be characterised by quality factor $Q = \frac{P_{L} + P_{C}}{P_{l o s s}} w$ .

Resonator losses can have different nature, including conductor losses, dielectric losses, radiation losses and others. Quality factor of a resonator is called unloaded $Q$ and assigned as $Q_{0}$ .

$Q_{0} = \frac{w_{0} L}{R} = \frac{1}{w_{0} R C}$ .

Resonator behaviour near it’s resonance frequency $Z_{i n} = R + j w L (\frac{w^{2} - w_{0}^{2}}{w^{2}})$ . $w^{2} - w_{0}^{2} = (w - w_{0}) (w + w_{0}) \approx 2 w ∆ w$ . Then $Z_{i n} = R + j w L \frac{2 w ∆ w}{w^{2}} = R + 2 j L ∆ w$ .

Then $Z_{i n} = R (1 + j \frac{Q ∆ w}{w_{0}})$ . Quality factor can also be a characteristics of a resonator bandwidth $\frac{1}{Q_{0}}$ .

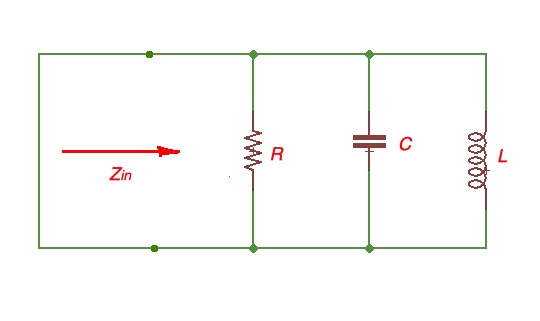
RLC parallel resonant circuit.

Here $\frac{1}{Z_{i n}} = (\frac{1}{R} + \frac{1}{j w L} - j w C)$ . As for the case above we calculate input power for resonator $P_{i n} = \frac{V I}{2} = \frac{1}{2 V^{2}} (\frac{1}{R} + \frac{1}{j w L} - j w C)$ . Resistor power losses are $P_{l o s s} = \frac{V^{2}}{2 R}$ . Energy stored in capacitor $P_{C} = \frac{V^{2} C}{4}$ , power stored in inductor $P_{L} = \frac{V^{2}}{4 w^{2} L}$ . As for the first example $P_{i n} = P_{l o s s} + 2 j w (P_{L} - P_{C})$ . And $Z_{i n} = \frac{2 P_{i n}}{I^{2}}$ .

When we have a resonance, $Z_{i n} = \frac{2 P_{l o s s}}{I^{2}}$ . Resonant frequency $w_{0} = \frac{1}{\sqrt{L C}}$ . Resonance in the parallel circuit is called anti-resonance.

Considering circuit frequencies close to resonant, and making similar calculations, $Q_{0} = \frac{R}{w_{0} L}$ . Knowing that $\frac{1}{1 + x} \approx 1 - x$ , then $Z_{i n} = \frac{1}{2 j C (w - w_{0})}$ and bandwidth $\frac{1}{Q_{0}}$ .

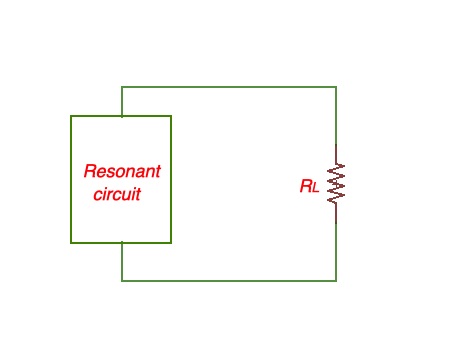
Cases above are for unloaded circuit. Let’s consider the case if the circuit is loaded as outlined below.

Let’s say the resonance circuit is loaded with the load resistor $R_{L}$ , then quality factor for external load is $Q_{e} = \{\begin{cases} \frac{w_{0} L}{R}, s e r i e s c o n n e c t i o n \\ \frac{R_{L}}{w_{0} L}, p a r a l l e l c o n n e c t i o n \end{cases}$ .

Then total quality factor is $Q = \frac{Q_{e} Q_{0}}{Q_{e} + Q_{0}}$ .