This post answers the question “What is meant by step-index and grade-index fibers?”. Geometrical fiber is the simplest type of fiber optics, has cylindric form with core and cladding layers. Cladding refractive index is lower that core refractive index.
These types of fibres differentiates with the way how refracting index is changing between cladding and the core:
- step-index fiber;
- graded-index fiber.
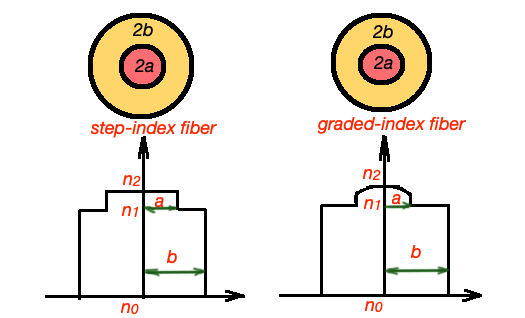
In case of step-index fiber the refractive index changes significantly. And in case of graded-index fiber, refractive index changes gradually.
This type of fiber optics works when the wavelength is much smaller than the core radius.
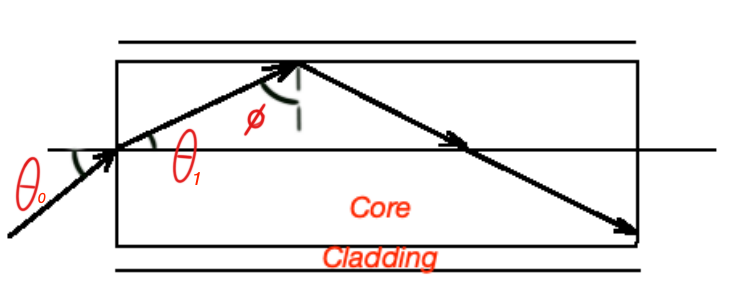
Let’s consider geometry of step-index fiber (below). Here . If we will follow the ray way – the initial ray is refracting on the border air-core, and refracting on the border core-cladding. The refraction on the border core-cladding is possible if the angle .
And , where is a numerical aperture .
These fibers are not very useful for communication purposes because of modal dispersion, when all the rays are spreading differently (with different angle in the fiber resulting different time dispersion at the output).
When multiple rays are traveling across the fiber, they can go through multiple lengths. Rays will end at the same time at the end of the fiber if they were travelled with the same speed.
Let’s consider an impulse through the fiber. We can calculate the time gap between the shortest and longest pathways of the dispersed rays through the fiber. The shortest pathway will be in case of , and the longest – for . If is a length of the fiber, then time difference between shortest and longest ray will be at the end of the fiber cable. This time difference is a measure of the signal broadening. This time difference should be less than a time slot . So . This relation is the limitation for step-index fibres.
Most fibres are designed so the ratio .
The gradual-index fibres are different from step-index ones. Here the refractive index is changing gradually from to value. Most graded-index fibers are designed towpath the -profile:
, here is a core radius.The most frequent fiber profile is graded-index profile, corresponding to , and is called parabolic-index profile.
The minimal dispersion corresponds to so and , where . The product of shows the quantitative characteristics of fiber, so it can be prepared the way to carry data with high bit rate to the long distances.
Read more content in our Reddit community r/ElectronicsEasy.