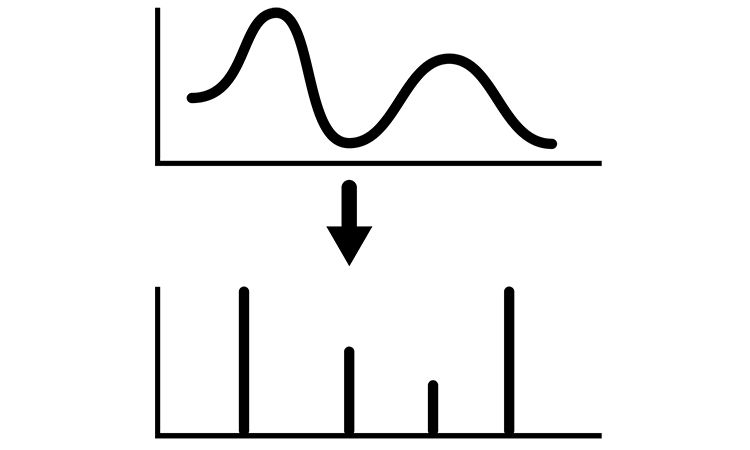
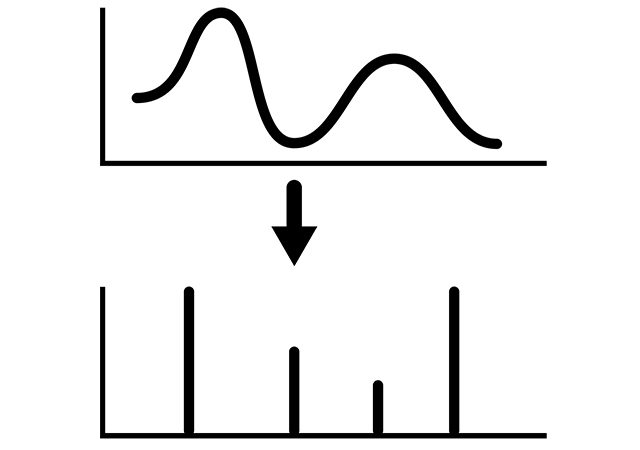
This post covers the topic of fourier transform for continuous signal. Let’s consider a Fourier representation of aperiodic signals. Let’s also consider an aperiodic signal as the piece of the periodic signal within a period, where the period is extremely large. The example of an aperiodic signal is depicted in Figure 1.
So, using the aperiodic signal, we can create a periodic signal. The Fourier representation of a periodic function is , . Here we can represent the signal envelope of the Fourier representation .
So using the signal envelope we can write down the periodic function as: . Applying here the condition of we can get the Fourier representation of an aperiodic signal , . The last two equations are a Fourier transform pair.
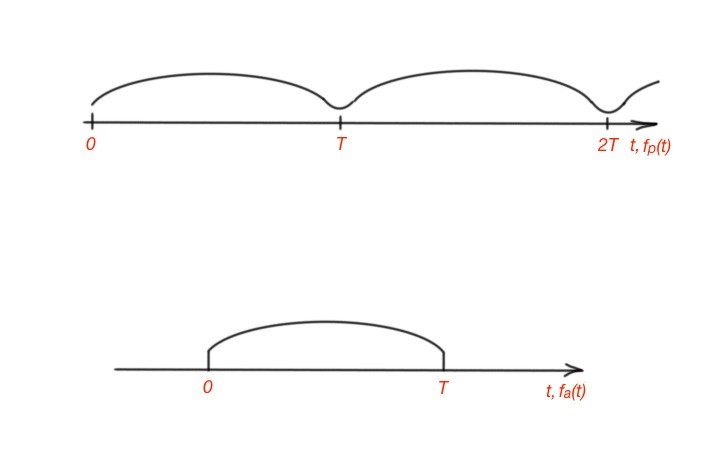 Figure 1. The example of periodic and aperiodic signals.
Figure 1. The example of periodic and aperiodic signals.
The discussed aperiodic function above should work satisfactorily in Dirichlet conditions. then we will know that the envelope is a finite function. In order to show that and are identical at the finite period of time, the three Dirichlet conditions should be right:
- ;
- should have a finite number of discontinuities on the finite interval of time;
- should have finite maximums and minimums within a finite time interval.
If we represent the periodic signal with a Fourier transformation as a set aperiodic signals (for example a set of impulse functions), here .
As we already know, the continuous-time periodic signal and its Fourier transformation are related to another with the Fourier transform synthesis equation: . Let’s think that and are a Fourier transformation pair. Taking into consideration the statements above we can formulate the properties of Fourier transformation for continuous-time periodic signals:
- Linearity. If there is two pairs of Fourier transformation , and , , so the following statement is valid:.
- Time shifting. If we have a pair of Fourier transformations and , after time shifting of the periodic signal, the Fourier transformation will be as follows: , and .
- Conjugation rule. If we have a Fourier transformation and , the conjugated Fourier transformation will be the following: and .
- Differentiation. If we have a Fourier transformation and , so for the differential of the periodic signal the Fourier transformation will be .
- Integration. If we have a Fourier transformation and , so for the integral of the periodic signal .
- Time scaling. If we have a Fourier transformation and , and α is the real number, so for a periodic function exists at a Fourier transformation of .
- Parseval’s formula. If and are Fourier transformations, so we have the following Parseval’s equation . Here is the energy density spectrum of the signal . So the energy of the signal can be calculated by integrating the signal over the time, or integrating the unit of energy over the frequency.
- Convolution. If we have two pairs of Fourier transformations , and , , so Fourier transformation for their convolution is: will be .
- Multiplication. If we have two pairs of Fourier transformations , and , so the Fourier transformation for the result of their multiplication will be H(jw)=. [1]
More educational tutorials can be accessed via Reddit community r/ElectronicsEasy.
{1] “Signals and systems”, 2nd edition, 1997. Alan V. Oppenheim, Allan S. Willsky.