Now we will study theorems which help to determine parameters of only a part of an electric circuit, for example current, voltage and power of a load resistor. These theorems allow replacement of the rest of a circuit as an equivalent source, what facilitates the task of a circuit analysis.
Thevenin’s theorem states that we can replace all the electric circuit, except a load resistor, as an independent voltage source in series, and the load resistor response will be the same. The Norton’s theorem states that we can replace the electric circuit except the load resistor as a current source in parallel.
It’s evident that the main use of these theorems is as a replacement of a part of a circuit to simplify the network and get rid of the part of the network which is not useful.
Let us consider the circuit in Figure 29. It’s separated on two parts – circuit with resistor RL, and circuit A, which can be simplified by making source transformations.
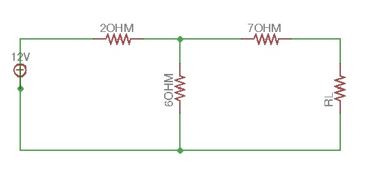
Let us make the following transformations – voltage source and 3Ohm resistor can be replaced as 3Ohm resistor and 4A current source in parallel. Parallel resistances will be transformed into 2Ohm resistance, and finally we can transform 4A current source and 2Ohm resistor into a resistor and voltage source in series. From the point of view of RL, the circuit did not change. However, it became simpler. This example lead us to the Thevenin’s Theorem:
As far as a load is concerned, any network composed of ideal voltage and current sources, and of linear resistors, may be represented by an equivalent circuit consisting of an ideal voltage source, in series with an equivalent resistance.
The Norton theorem states the following:
As far as a load is concerned, any network composed of ideal voltage and current sources, and of linear resistors, may be represented by an equivalent circuit consisting of an ideal current source, in parallel with an equivalent resistance.