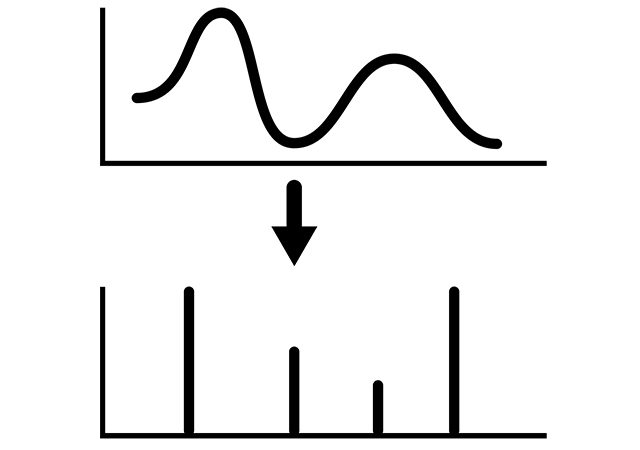
This post answers the question “What is the difference between continuous and discrete signal?” From a general point of view, signals are functions of one or several independent variables. There are two types of signals – discrete-time and continuous-time signals. Discrete-time signals are defined at the discrete moment of time and the mathematical function takes the discrete set of values.
Continuous-time signals are characterised by independent variables that are continuous and define a continuous set of values. Usually the variable indicates the continuous time signals, and the variable n indicates the discrete-time system. Also the independent variable is enclosed at parentheses for continuous-time signals and to the brackets for discrete-time systems. The feature of the discrete-time signals is that they are sampling continuous-time signals.
The signals we are describing are obviously related to the features of the system as power and energy. The total energy of the continuous-time signal over the interval is .
Here is the magnitude of the function .
Here the brackets are describing the time-continuous interval . The parentheses can be used for describing the time-continuous interval . The continuous-time power can be obtained by deriving the energy by the time interval .
The total energy of the discrete-time signal over the interval is the sum .
Where the average power over the indicated interval can be obtained with energy derived by the .
Many systems exist over the infinite interval of the independent variable. For these systems
For continuous-time, and
Some integrals and sums may not converge. These systems are characterised by the infinite energy . For converging integrals and sums, signals have a finite energy .
The average power for discrete-time and continuous-time signals for an infinite period of time are:
The signals with a finite total energy are characterised with zero average power . The signals with infinite total energy are characterised by .
We are considering here the most simple and frequent variable transformations that can be combined, resulting in complex transformations.
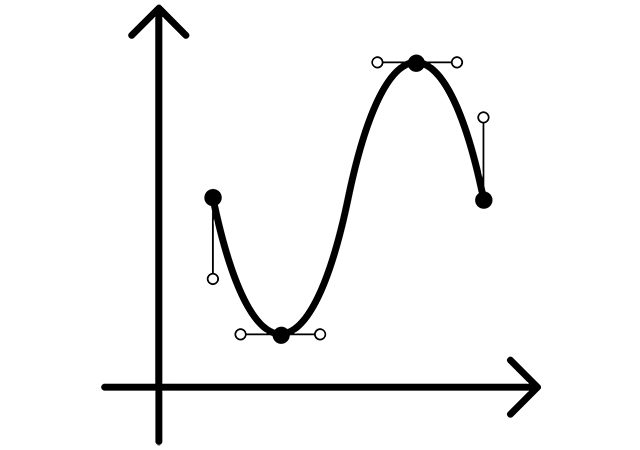
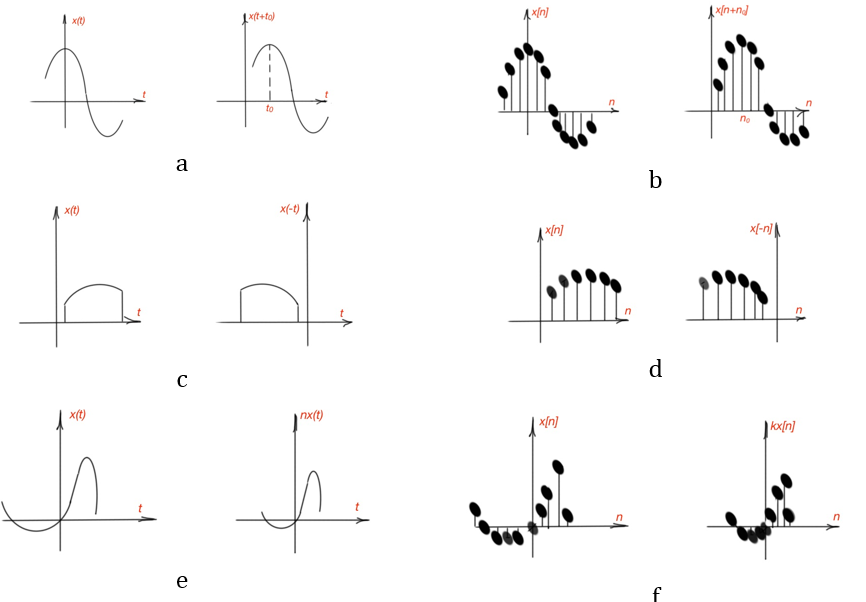
- Time shift is the transformation when two signals and are the same but are displaced relatively to each other. The same for time-continuous signals and .
- Time reversal is when the signal is obtained from by reflecting the signal relatively . For continuous-time signals is a reflection over .
- Transformation , is where and are given numbers. Here the transformation depends on the value and sign of numbers, so if and the signal is extended, if and the signal is compressed, if , the signal is reversed and can be extended or compressed, depending on the magnitude and sign of the signal is shifted right or left. For discrete-time variables the transformations are the same .
Figure 1 depicts different kinds of signal transformations for continuous-time and discrete-time variables.
Periodic signals.
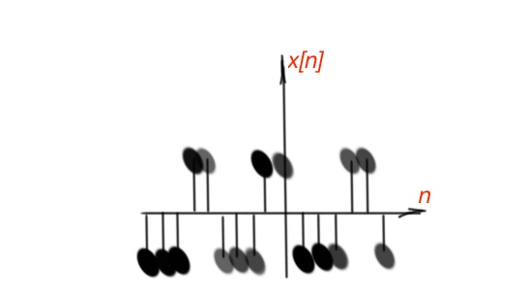
The periodic discrete-time signals with the period , where is the positive integer number, are characterised by the feature for all values. This equation also works for , … period. The fundamental period is the smallest period value where this equation works. Figure 2 depicts an example of discrete-time periodic signal.
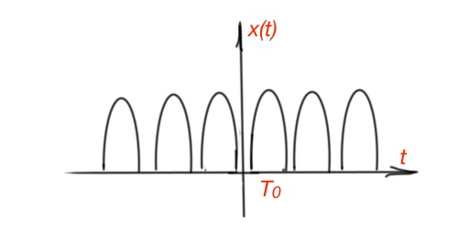
The continuous-time periodic signals with period , are characterised by the feature . Also we can deduce that , where is an integer number. The fundamental period is the smallest period value where this equation works. Figure 3 depicts an example of discrete-time periodic signal.
Even and odd signals.
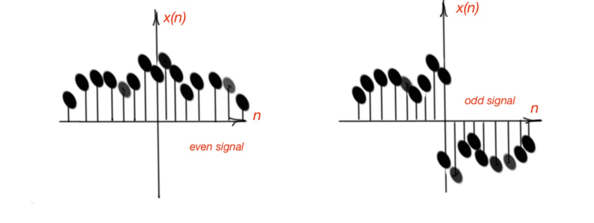
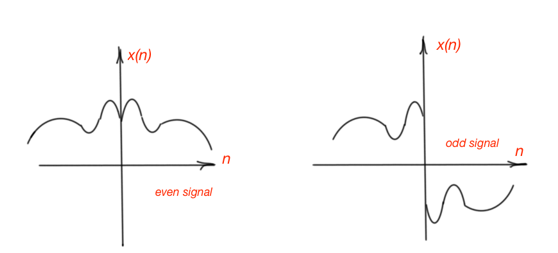
The discrete-time signal and continuous-time signal are even if they are equal to their time-reversed counterparts, and . And the signals are odd, if and . Odd signals are always 0 when , or .
Figures 4 and 5 depict even and odd discrete- and continuous-time signals.
Any continuous-or discrete-time signals can be presented as a sum of odd and even signals. For continuous-time signals:
for discrete-time signals:
More educational tutorials can be accesses as well via Reddit community r/ElectronicsEasy.