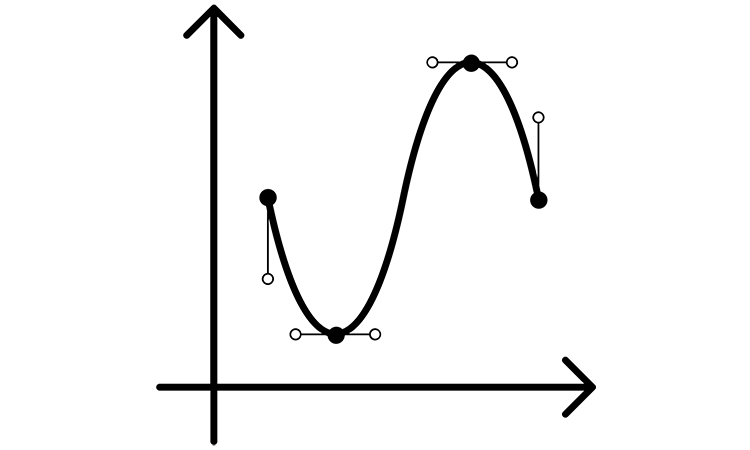
This post answers the question “What is discrete LTI system?”. It is useful to consider discrete-time signals as a sequence of impulses. For example, a discrete-time signal is on show in Figure 1. Figure 2 shows its mathematical representation, where the signal is divided into the single impulses. S, the sum of these individual impulses, form the initial discrete-time signal.
The sum of the impulses is: . In the other words the discrete-time signal is the linear combination of shifted impulses with the weight . This equation is called the shifting property of the discrete-time unit impulse.
![The mathematical representation of the discrete-time function x[n].](https://www.student-circuit.com/wp-content/uploads/sites/54/2018/08/figure1.jpg)
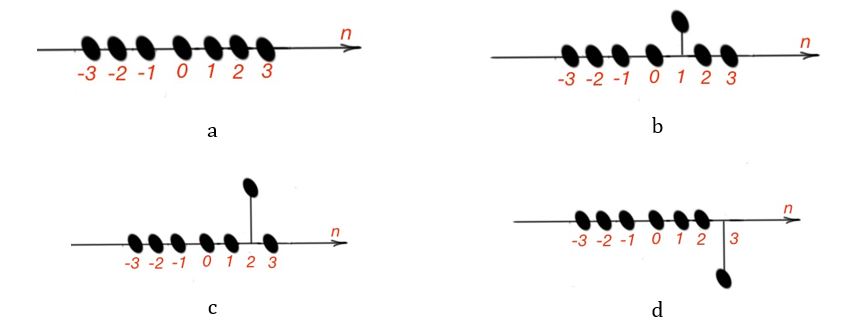
Let’s consider the response of a linear discrete-time function x[n], that can be represented by the sum of impulses , i.e. a linear combination of weighted shifted impulses.
If the input of the linear system is , then the output . Here the are the responses to the signals .
Generally speaking, the functions are not related to each other for each particular . In our case is a response of impulse function, then is a linear shifted version of itself.
So . Let’s assume that . is the output for the input of the LTI system. So we have . This equation is called superposition (convolution) sum of the sequences and . Symbolically superposition(convolution) function is represented by .
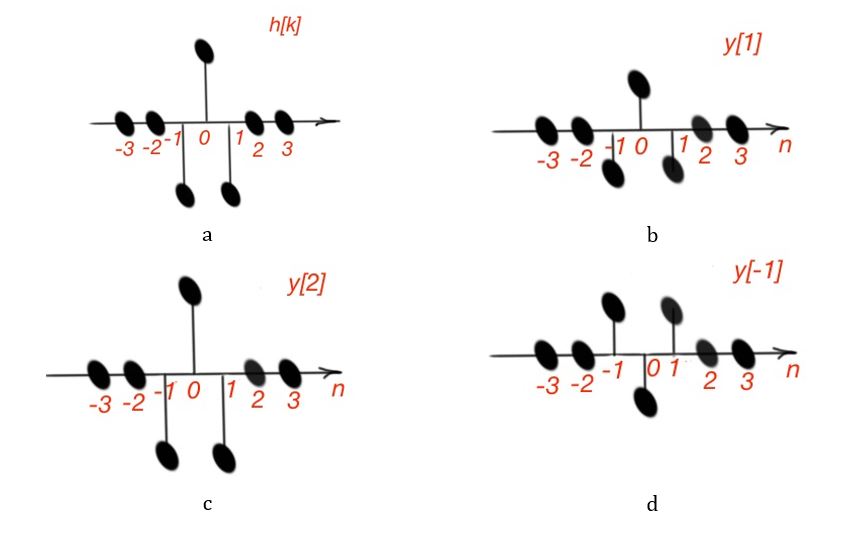
1. Determine the function ;
2. Determine the function .
More educational tutorials can be accessed via Reddit community r/ElectronicsEasy.