Electromagnetic induction

In 1831 British physicist Michael Faraday was analysing all the cases of electromagnetic induction phenomena – phenomena of current induction in a conductor along the magnetic field. As the source of a magnetic field, magnetics and induction was used as a circuit. Second induction was used for detecting induction currents.

When the ‘registering inductance’ was in the field of a static magnet, there were no induction currents, regardless of the magnitude of current through the circuit 1.

When the magnet or registering inductance of the circuit 2 were moving, inducing current appeared through the inductance 2. Also the inducing current in the ‘registration inductance’ appeared when the magnet field from a magnet was changed, or current through the induction 1 was changed. Faraday made the important conclusion from this series of experiments that electric current inducing in the magnetic field is the result of the magnetic flow change.

Even flexible deformation of the inductor can provoke the inducing currents in the magnetic field. Induction of the electric current in the conducting circuit occurs as the result of a magnetic field flow change through the surface – limited by this circuit. Experiments led Faraday to the conclusion that the inducing current in the circuit has the following formula:

Magnetic flow is the flow of the magnetic induction

Integral to this is the algebraic sum of the flow of magnetic induction in every point of a closed surface.

The Lentz rule: Magnetic field generated by the circuit with an electric current is directed in a way that hinders the external magnetic field.

<strong>Electromagnet induction law (The law of Fradei-Maxwell)</strong>

Induction of EMF in the dynamic conductors. Induction current in the conductor appears as the result of self-electromotive force phenomena – induction current magnitude

$I_{i}nd=\frac{{\epsilon }_{i}nd}{R}$

where R is the resistance of the circuit. The law of electromagnetic induction in the conducting circuit states that self-electromotive force (self-EMF) magnitude is equal to the magnetic flow rate through the surface, enclosed by the circuit.

${\epsilon }_i=–\frac{d\Phi }{dt}$

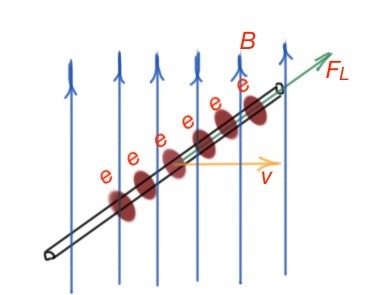
This formula has a negative sign, what is stated by the Lentz rule. Let’s consider a conduction stick, moving in the magnetic field perpendicular to its lines. Figure 32. There is a difference in potential that occurs between the parts of this stick. This stick experiences the charge division. So what makes these charges divide? The answer is the Lorentz Force. As free electrons experience the movement with speed v in the magnetic field of the Earth, EMF of electromagnetic induction will be equal to the Lorentz force – A = qvBl and

${\epsilon }_i=\frac{qvBl}{q}=vBl$

#12 Self-induction – Inductivity