Module aims Microcontrollers serve as fundamental elements in embedded systems and the Internet of Things (IoT). This unit imparts a foundational understanding of microcontroller…
Category: Year 1
Year 1: digital system design level 1
Module aims This module aims to acquaint students with the basics of designing combinatorial and sequential logic circuits. It serves as a foundation for…
Year 1: electronic materials
Module aims The objectives of this course module are as follows: Provide an initiation into nanotechnology and underscore its significance in contemporary society, highlighting…
How does surge suppression work?
This post answers the question "How does surge suppression work?". When an engineer wants to provide the highest level of safety and reliability of your…
Analog divider and multiplier
This post tells about analog divider and multiplier and covers an introduction to voltage divider and multiplier. The voltage divider and multiplier are considered…
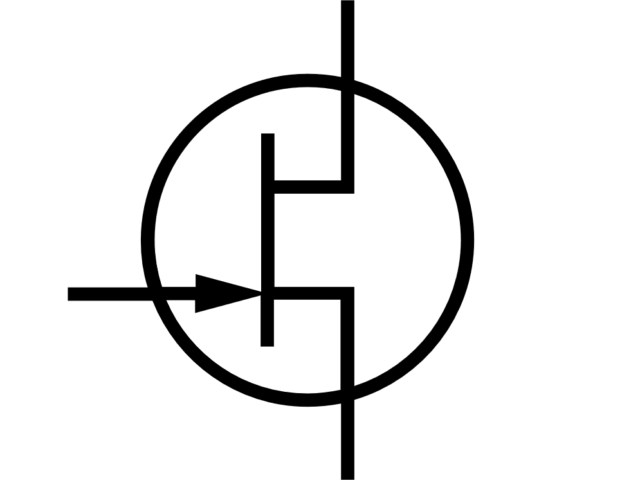
What is a JFET transistor and how it works
This post is about structure, parameters and properties of JFET transistor. JFET transistor is a three-terminal device, where one of the terminal can control…
Complex numbers
Definition of complex number A Complex number is a pair of real numbers (x;y). Its algebraic form is z=x+i*y, where i is an imaginary…
Complex numbers 2
Let's suggest a function y=f(x) that is defined on the interval (a,b). Choose a point x on the interval (a,b), and another point x+∆x…
Differentiability, differential of a function and integral
If function y=f(x) has a derivative in the point x: lim∆x→0 ∆y∆x=f' (x) Let's introduce the function: α(x)=∆y∆x-f' (x)=f(x+∆x)-f(x)∆x-f' (x) Function α(x) exists with the…
Quiz
Solve this quiz and write your answers in comments. Exercise 1. Calculate: a. 5-1i3+i;b. (7+2i)-(3-2i)+(11+i)-(17-3i);c. (2+i)*(5-2i)+(6+13i)*(7-i);d. -13+6i2-i+ (8-i5+2i)2 Exercise 2. Calculate: Re(12-i6+3i), Im(-2i5+i) Exercise 3. Find all…